Leetcode 15번 문제 3Sum 을 풀어보겠습니다.

이번 3Sum 문제는 중 난이도 로 릿코드 1번 문제인 투썸과 비슷하지만 3개의 숫자의 합이 0이 되는 배열을 리턴해야 하는 문제입니다.
문제설명
Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
Notice that the solution set must not contain duplicate triplets.
Example 1:
Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]
Explanation:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
The distinct triplets are [-1,0,1] and [-1,-1,2].
Notice that the order of the output and the order of the triplets does not matter.
Example 2:
Input: nums = [0,1,1]
Output: []
Explanation: The only possible triplet does not sum up to 0.
Example 3:
Input: nums = [0,0,0]
Output: [[0,0,0]]
Explanation: The only possible triplet sums up to 0.
Constraints:
- 3 <= nums.length <= 3000
- -105 <= nums[i] <= 105
위 1번 예제처럼 Output인 [[-1, -1, 2], [-1, 0, 1]] 두 배열의 모든 원소의 합은 0 입니다.
먼저 모든 경우의 수를 가지고 접근해 보겠습니다.
모든 경우의 수를 계산하려면 for loop 를 세 번 쓰면 될 듯 합니다(brute-force)
문제풀이
Brute-force 접근
코드부터 살펴보겠습니다.
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
nums.sort((a, b) => a - b);
const result = [];
for(let i=0; i<nums.length; i++) {
for(let j=i+1; j<nums.length; j++) {
for(let k=j+1; k<nums.length; k++) {
if (nums[i] + nums[j] + nums[k] === 0)
result.push([nums[i], nums[j], nums[k]]);
}
}
}
return result;
};일단 이렇게 짜 보았습니다.
i, j, k 변수를 이용해서, j는 i+1, k는 j+1을 시작으로 해서 모든 3가지 경우의 조합을 생각해서 합이 0이면 result 배열에 push 하는 방식입니다.

이 방법의 경우 Testcase1번이 Fail 했네요.
[-1, 0, 1] 의 배열이 두 번 들어갔습니다.
이것은 예제 1번의 경우 -1인 원소가 두번 들어있는데 두 번 모두 어떠한 체크도 없이 모든 원소를 순차적으로 돌기 때문에 자동적으로 증가가 된 것입니다.
중복된 인덱스를 push 하지 않도록 if, continue 를 넣어서 아래와 같이 작성했습니다.
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
nums.sort((a, b) => a - b);
const result = [];
for(let i=0; i<nums.length; i++) {
if (i>0 && nums[i-1] === nums[i]) continue;
for(let j=i+1; j<nums.length; j++) {
if (j>i+1 && nums[j-1] === nums[j]) continue;
for(let k=j+1; k<nums.length; k++) {
if (k>j+1 && nums[k-1] === nums[k]) continue;
if (nums[i] + nums[j] + nums[k] === 0)
result.push([nums[i], nums[j], nums[k]]);
}
}
}
return result;
};먼저, nums[i-1] 과 nums[i] 의 값이 같다면 정렬된 nums 배열에서 같은 원소가 들어있는 경우 이므로 이 경우에 continue 를 써서 바로 for 문을 나와 i 인덱스를 하나 증가시켜줘야 할 것입니다.
그런데, i가 0일경우 nums[-1] 가 되므로 인덱스에서 오류가 나기 때문에 먼저 i가 0보다 큰 수 인지 확인을 해줍니다.
마찬가지로 j, k 도 처음 initialize 된 값인 i+1, j+1 보다 큰지를 먼저 검사한 후 두 값이 연속이 되는지를 체크해줍니다.
같을 경우 마찬가지로 해당 인덱스를 1 증가시킵니다.
if문에서 모두 false 가 날 경우 최종적으로 세 인덱스의 수의 합이 0이 되는지를 검사하고 그렇다면 result 배열에 푸시해줍니다.
모든 루프가 돌면 result 를 리턴하면 됩니다.
Brute-force 성능
코드를 Submit 했더니 꽤 오래 걸립니다.

Time Limite Exceeded 가 뜹니다.
지금 for loop 가 세개가 nested 되어 돌기 때문에 시간 복잡도가 O(n^3) 이 되어있어서 테스트케이스 312개 중 하나가 Fail 한 모습입니다.
시간복잡도를 해결하기 위해 다른 방법으로 접근해 보겠습니다.
Two Pointer 접근
투포인터를 써서 접근해보겠습니다.
이 방법같은 경우 제일 처음의 for loop 는 유지합니다.
그 다음에 비교되는 숫자들은 left, right 에 할당해서 세 숫자의 합이 0보다 큰지, 작은지, 같은지 여부에 따라 포인터를 옮기며 찾는 것입니다.
left 는 i+1의 인덱스를 처음 가지고, right 는 nums.length - 1 (마지막값)을 첫 값으로 가집니다.
예를 들어 예제 1번을 살펴보겠습니다.
nums = [-1,0,1,2,-1,-4]처음에 정렬을 하고 해야 하므로 정렬된 값을 밑에 표시하겠습니다.
nums = [-4,-1,-1,0,1,2]| i | nums[i] | left | nums[left] | right | nums[right] | nums[i] +nums[left] +nums[right] |
result |
| 0 | -4 | 1 | -1 | 5 | 2 | -3 | 0보다 작으므로 left+1 |
| 2 | -1 | nums[left]가 nums[left+1]과 같으므로 left++ 가능 nums[i]+nums[left]+nums[right] 체크 불필요 |
|||||
| 3 | 0 | -2 | 0보다 작으므로 left+1 | ||||
| 4 | 1 | -1 | 0보다 작으므로 left+1 이지만 0이 right와 값이 같아지므로 다음 i 인덱스로 | ||||
| 1 | -1 | 1(초기화) | -1 | 5(초기화) | 2 | 0 | 0이므로 result에 추가 result = [[-1, -1, 2]] |
| 2 | -1 | nums[left]가 nums[left+1]과 같으므로 left++ 가능 이미 세 합이 0이되어 push되었으므로 left++ |
|||||
| 3 | 0 | 1 | 0보다 크므로 right-1 | ||||
| 4 | 1 | 0 | 0이므로 result에 추가 resut = [[-1, -1, 2], [-1, 0, 1]] |
||||
| 이런식으로 정렬이 되어 있으므로 i 인덱스는 고정시킨 상태에서 left와 right의 합과 0을 비교해가며 음수면 left를 증가, 양수면 right를 감소시키는 방식으로 쭉 돌면 모든 result 가 추가 됩니다. | |||||||
코드로 살펴보겠습니다.
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
const result = [];
nums.sort((a, b) => a - b);
for (let i=0; i<nums.length-2; i++) {
if (nums[i] > 0) break;
if (i>0 && nums[i] === nums[i-1]) continue;
let left = i+1;
let right = nums.length-1;
while(left < right) {
let sum = nums[i] + nums[left] + nums[right];
if (sum === 0) {
result.push([nums[i], nums[left], nums[right]]);
while (nums[left] === nums[left+1]) left++;
while (nums[right] === nums[right-1]) right--;
left++;
right--;
} else if (sum < 0) {
left++;
} else
right--;
}
}
return result;
};우선 정렬을 해주고 첫번째 인덱스부터 시작해서, 정렬된 첫번째 인덱스부터 0 이상이면 어떠한 조합으로도 세 수의 합이 0이 될 수 없으므로 바로 break를 걸고 빈 배열을 리턴합니다.
아닐 경우에는 i 기준으로는 같은 값을 add 하면 안되기 때문에 if continue 를 넣어줍니다.
left, right 를 각각 인덱스로부터 오른쪽, 배열의 마지막으로 설정을 합니다.
오른쪽 포인터(right)는 큰 값이므로 sum이 크게 되면 이 값을 왼쪽으로 하나 (1 decrement) 옮기면 되겠죠?
마찬가지로 왼쪽 포인터(left)는 작은 값이므로 sum이 크게 되면 이 값을 오른쪽으로 하나 (1 incremenet) 옮기면 되겠죠?
역시 예제 1을 기준으로 한번 포인터에 중점에 맞춰서 설명해보겠습니다.
nums = [-4,-1,-1,0,1,2]| -4 | -1 | -1 | 0 | 1 | 2 |
| i | left | right | |||
| left | right | ||||
| left | right | ||||
| left | right | ||||
| right | left | ||||
| i | left | right | |||
| left | right | ||||
| left | right (합 0, result) | ||||
| right | left | ||||
| i | left | right | |||
| left | right (합 0, result) | ||||
| right | left | ||||
| i | left | right | |||
| right | left |
위 표와 같이 i는 순서대로 증가하고, left, right 는 합에 따라 왼쪽, 오른쪽으로 옮겨가며 left 와 right 가 교차 되었을 때 다음 i 루프를 계속 돌면 모든 경우의 수의 합을 구할 수 있습니다.
특히 두번째 줄의 경우 2번째 인덱스(i===1, nums[i] === -1)이 3번째 인덱스와 값이 -1로 같으므로 이런 경우에는 맨 안쪽 while 루프 안에서 계속 포인터를 옮겨 줌으로써 불필요한 sum을 계산 안하는 동시에 result array 에 push도 하지 않는 효율적인 코드 입니다.
투포인터 성능
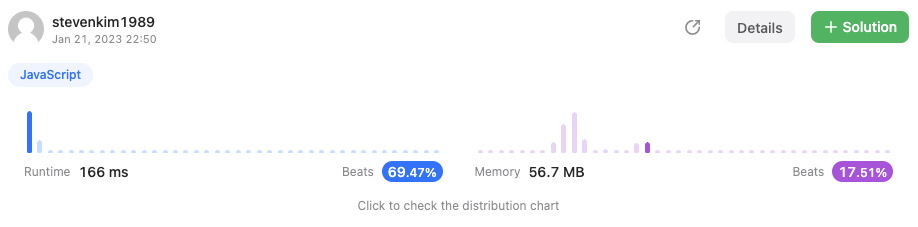
이상으로 3Sum 문제를 풀어보았습니다.
※ 앞으로 모든 문제를 JavaScript 로 올릴 예정입니다.
릿코드 연습을 하며 올린 포스팅이므로 간혹 틀린 부분이 있을 수 있습니다.
혹시 잘못된 부분이 있을 경우 댓글 남겨주시면 감사드리겠습니다.
다른 문제 풀이도 깃헙에서 확인 할 수 있습니다.
'Software Development > Leetcode' 카테고리의 다른 글
| 릿코드 121번 문제 Best Time to Buy and Sell Stock 자바스크립트 문제 해석 및 풀이 Leetcode 11 Javascript (1) | 2023.01.25 |
|---|---|
| 릿코드 11번 문제 Container With Most Water 자바스크립트 문제 해석 및 풀이 Leetcode 11 Javascript (0) | 2023.01.23 |
| Leetcode 125. Valid Palindrome (0) | 2023.01.19 |
| Leetcode 128. Longest Consecutive Sequence (0) | 2023.01.19 |
| Leetcode 271. Encode and Decode Strings (0) | 2023.01.19 |




댓글